
기하학, 듣기만 해도 왠지 어렵고 복잡하게 느껴지죠? 사실 기하학은 우리 주변 세상을 이루는 기본적인 형태와 공간을 다루는 아주 재밌는 학문이에요. 특히, 위상수학이라는 분야에서는 공간의 기본적인 성질, 즉 ‘연결’과 ‘구멍’에 초점을 맞춰 공간을 연구한답니다. 오늘은 그중에서도 연결성과 단순 연결성이라는 개념을 파헤쳐 보고, 왜 이렇게 중요한지, 그리고 우리 생활과 어떤 관련이 있는지 알아볼 거예요.
연결성: 공간을 하나로 이어주는 끈

연결성이라는 건 쉽게 말해, 어떤 공간이 끊어지지 않고 하나로 이어져 있는지를 나타내는 거예요. 마치 끊어지지 않은 실처럼 말이죠. 좀 더 수학적으로 얘기하자면, 어떤 공간을 두 개의 겹치지 않는 부분으로 나눌 수 없을 때, 그 공간은 연결되어 있다고 합니다.
연결성의 다양한 모습

연결성을 나타내는 방법은 여러 가지가 있어요. 그중에서도 경로 연결성이라는 개념이 꽤 흥미로운데요, 이건 공간 안의 아무 두 점이나 끊어지지 않는 선으로 연결할 수 있을 때를 말해요. 마치 지도에서 두 도시를 연결하는 도로처럼요.
예를 들어 볼까요?
- 원(circle)은 연결된 공간이에요. 아무리 잘라보려고 해도 두 개의 분리된 부분으로 나눌 수 없거든요.
- 두 개의 원(two circles)은 연결되지 않은 공간이에요. 두 원 사이의 빈 공간을 이용해서 두 개의 분리된 부분으로 나눌 수 있기 때문이죠.
- 직선(line)도 연결된 공간이에요. 직선을 아무리 잘라봐도 두 개로 나눌 수 없으니까요.
하지만 연결성만으로는 공간의 특징을 완벽하게 나타낼 수 없다는 게 함정! 그래서 등장한 개념이 바로 단순 연결성이랍니다.
단순 연결성: 공간 속 숨겨진 구멍 찾기

단순 연결성은 연결성보다 좀 더 까다로운 조건을 갖춘 개념이에요. 연결되어 있는 것만으로는 부족하고, 공간 안에 구멍이 없어야 한다는 조건이 추가되는 거죠.
단순 연결성의 핵심: 폐곡선의 수축

이게 무슨 말일까요? 쉽게 생각해 보면, 공간 안에 아무렇게나 그린 곡선을 점점 줄여서 하나의 점으로 만들 수 있다면, 그 공간은 단순 연결된 공간이라고 할 수 있어요.
핵심은 ‘폐곡선’이에요. 폐곡선이란 시작점과 끝점이 같은 곡선을 말하는데, 이 폐곡선을 점점 줄여서 한 점으로 만들 수 있다면, 그 공간은 구멍이 없다는 뜻이 되는 거죠. 마치 고무줄을 점점 줄여서 한 점으로 만드는 것과 비슷해요.
예시를 통해 좀 더 명확하게 이해해 볼까요?
- 구면(sphere)은 단순 연결된 공간이에요. 구면 위의 아무 폐곡선이나 점점 줄여서 한 점으로 만들 수 있거든요.
- 원(circle)은 단순 연결되지 않은 공간이에요. 원을 한 바퀴 도는 폐곡선은 점점 줄여서 한 점으로 만들 수 없어요.
- 도넛(torus) 또한 단순 연결되지 않아요. 도넛의 구멍을 한 바퀴 도는 폐곡선은 점점 줄여서 한 점으로 만들 수 없거든요.
연결 성분: 공간을 나누는 조각들

위상 공간은 여러 개의 연결된 부분으로 나뉘어질 수 있어요. 이때, 각 부분을 연결 성분(connected component)이라고 부른답니다. 연결 성분은 위상 공간을 분할하는 데 사용할 수 있으며, 각 연결 성분은 서로 겹치지 않아요.
예를 들어, 두 개의 원(two circles)은 두 개의 연결 성분을 가지고 있어요. 각 원이 하나의 연결 성분이 되는 거죠.
위상동형: 공간의 본질을 꿰뚫는 눈

위상동형(homeomorphism)은 두 위상 공간 사이의 특별한 관계를 나타내는 개념이에요. 두 공간이 위상동형이라는 것은, 두 공간 사이에 일대일 대응 관계가 존재하고, 이 대응 관계와 그 역함수가 모두 연속적일 때를 말해요. 쉽게 말해, 위상동형인 두 공간은 본질적으로 같은 모양을 갖고 있다고 볼 수 있답니다.
위상동형의 특징: 변형의 마법

위상동형은 공간을 늘리거나 줄이거나 구부리는 등의 변형을 허용하지만, 찢거나 붙이는 등의 변형은 허용하지 않아요. 마치 찰흙으로 여러 가지 모양을 만들 수 있지만, 찰흙을 찢거나 붙이지는 않는 것과 비슷하죠.
예를 들어, 원(circle)과 타원(ellipse)은 위상동형이에요. 원을 늘이거나 줄여서 타원으로 만들 수 있거든요. 하지만 구면(sphere)과 원판(disk)은 위상동형이 아니에요. 원판을 아무리 늘리거나 줄이거나 구부려도 구면을 만들 수 없으니까요.
위상동형과 연결성, 단순 연결성의 관계

위상동형은 연결성과 단순 연결성을 보존하는 중요한 특징을 가지고 있어요. 즉, 두 공간이 위상동형이라면, 한 공간이 연결되어 있다면 다른 공간도 연결되어 있고, 한 공간이 단순 연결되어 있다면 다른 공간도 단순 연결되어 있답니다.
예시를 들어 볼게요.
- 원(circle)과 타원(ellipse)은 위상동형이고, 둘 다 연결되어 있으며 단순 연결되어 있지 않아요.
- 구면(sphere)은 토러스(torus)와 위상동형이 아니에요. 구면은 단순 연결되지만, 토러스는 단순 연결되지 않거든요.
연결성과 단순 연결성의 실생활 적용
이제 연결성과 단순 연결성이 우리 생활과 어떤 관련이 있는지 알아볼까요? 사실 우리 주변에는 연결성과 단순 연결성의 개념이 숨겨져 있는 경우가 정말 많답니다.
네트워크: 연결의 힘

인터넷이나 소셜 네트워크 서비스(SNS)와 같은 네트워크는 연결성을 기반으로 한 대표적인 예시에요. 네트워크의 노드(node)들이 서로 연결되어 정보를 주고받을 수 있도록 하는 것이죠. 네트워크의 연결성이 높을수록 정보 전달이 빠르고 효율적이 된답니다.
도시 계획: 사람들의 이동을 돕는 연결

도시를 설계할 때, 도로, 지하철, 건물 등의 연결성을 고려하는 것도 중요해요. 사람들이 편리하게 이동하고, 다양한 시설을 이용할 수 있도록 연결성을 최대화하는 것이 도시 계획의 중요한 목표 중 하나죠.
전력망: 끊김없는 전력 공급

전력망은 발전소, 송전탑, 변전소, 가정 등이 서로 연결되어 전력을 공급하는 네트워크예요. 전력망의 연결성이 높을수록 전력 공급이 안정적이고, 고장 발생 시에도 다른 경로를 통해 전력을 공급할 수 있답니다.
3D 모델링: 가상 세계를 만드는 연결
3D 모델링에서 연결성은 객체의 표면을 구성하는 면들이 서로 연결되어 있는지를 나타내요. 연결성이 끊어져 있으면 객체의 표면에 구멍이 생기거나, 3D 프린팅 시 오류가 발생할 수 있답니다.
로봇 경로 계획: 장애물을 피해가는 연결

로봇이 장애물을 피해 목표 지점까지 이동하는 경로를 계획할 때, 로봇이 이동할 수 있는 공간의 연결성을 고려해야 해요. 로봇이 이동할 수 있는 경로가 끊어져 있으면 로봇이 목표 지점까지 이동할 수 없게 되죠.
연결성과 단순 연결성 개념 정리
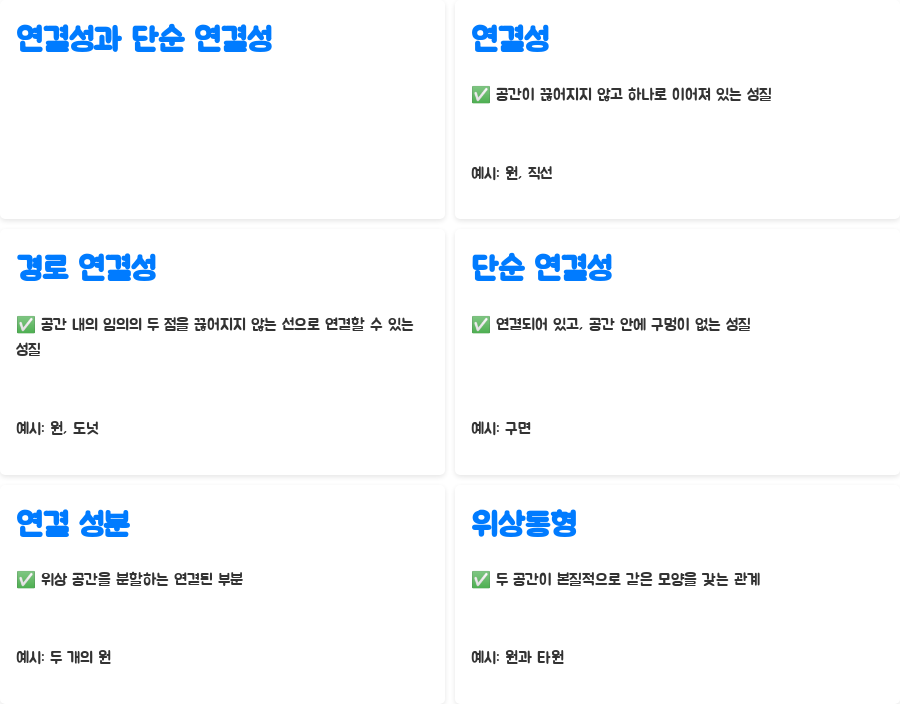
| 연결성 | 공간이 끊어지지 않고 하나로 이어져 있는 성질 | 원, 직선 |
| 경로 연결성 | 공간 내의 임의의 두 점을 끊어지지 않는 선으로 연결할 수 있는 성질 | 원, 도넛 |
| 단순 연결성 | 연결되어 있고, 공간 안에 구멍이 없는 성질 | 구면 |
| 연결 성분 | 위상 공간을 분할하는 연결된 부분 | 두 개의 원 |
| 위상동형 | 두 공간이 본질적으로 같은 모양을 갖는 관계 | 원과 타원 |
개념 설명 예시
마무리하며

오늘은 위상수학에서 매우 중요한 개념인 연결성, 단순 연결성, 위상동형, 그리고 이들이 실생활에서 어떻게 활용되는지에 대해 알아보았어요. 이 개념들은 공간의 구조와 성질을 이해하는 데 핵심적인 역할을 하며, 다양한 분야에서 활용되고 있습니다. 특히 위상동형은 공간의 본질적인 성질을 유지하면서 변형을 고려할 수 있게 해주는 중요한 도구임을 기억해두면 좋아요. 이 글을 통해 연결성, 단순 연결성, 위상동형, 그리고 실생활 적용에 대한 이해가 좀 더 깊어졌기를 바라요!
자주 묻는 질문 (FAQ)
Q1. 연결성과 단순 연결성의 차이점은 뭐에요?
A1. 연결성은 공간이 하나로 이어져 있는지를 나타내는 반면, 단순 연결성은 연결되어 있으면서 동시에 공간 안에 구멍이 없어야 한다는 더 엄격한 조건을 갖추고 있어요.
Q2. 위상동형이 왜 중요한가요?
A2. 위상동형은 두 공간이 본질적으로 같은 모양을 갖는지를 판단하는 기준이 되기 때문에, 공간의 기본적인 성질을 이해하는 데 매우 중요해요. 또한, 위상동형을 통해 연결성과 단순 연결성과 같은 중요한 성질이 보존되는지 확인할 수 있답니다.
Q3. 실생활에서 연결성과 단순 연결성을 어떻게 활용할 수 있나요?
A3. 연결성과 단순 연결성은 네트워크, 도시 계획, 전력망, 3D 모델링, 로봇 경로 계획 등 다양한 분야에서 활용될 수 있어요. 특히, 시스템의 안정성, 효율성, 효과적인 연결을 확보하는 데 중요한 역할을 한답니다.
키워드:기하학,위상수학,연결성,단순연결성,위상동형,수학,공간,구조,성질,네트워크,도시계획,전력망,3D모델링,로봇,경로계획,폐곡선,수축,연결성분,수학공부,과학,공학,데이터분석


댓글