음… 다면체, 뭔가 딱딱하고 복잡해 보이죠? 정육면체, 정사면체, 정팔면체… 이름만 들어도 머리가 지끈지끈할 것 같아요. 하지만 이 다면체 속에는 생각보다 흥미로운 비밀이 숨겨져 있답니다. 바로 오일러의 다면체 정리라는 거예요. 이 정리는 18세기, 위대한 수학자 레온하르트 오일러가 발견한 건데, 다면체의 꼭짓점, 모서리, 면의 개수 사이에 엄청나게 간단하면서도 아름다운 관계가 있다는 걸 보여주죠.
오일러의 다면체 정리: 다면체의 숨겨진 관계

오일러는 다면체의 꼭짓점을 V, 모서리를 E, 면을 F라고 표현했어요. 그리고 이 셋 사이의 관계를 다음과 같은 공식으로 나타냈답니다.
V - E + F = 2? 정말 간단하죠? 이 공식을 오일러 공식이라고 부르는데, 이 공식은 다면체의 모양이나 크기에 상관없이 항상 성립한다는 게 정말 신기해요.
예를 들어, 정육면체를 생각해 볼까요? 정육면체는 8개의 꼭짓점, 12개의 모서리, 6개의 면을 가지고 있어요. 이 값들을 오일러 공식에 대입해 보면, 8 - 12 + 6 = 2가 되는 걸 확인할 수 있죠.
다른 다면체들도 마찬가지에요. 삼각뿔(사면체)는 4개의 꼭짓점, 6개의 모서리, 4개의 면을 가지고 있고, 4 - 6 + 4 = 2가 되네요. 이렇게 다양한 다면체에서 오일러 공식이 항상 성립한다는 사실은 정말 놀랍죠!
오일러 공식 증명: 다면체의 비밀을 밝히다

그럼 이 공식이 왜 항상 성립하는 걸까요? 궁금증이 생기죠? 오일러 공식은 다양한 방법으로 증명될 수 있는데, 그중 하나를 간단하게 소개해 드릴게요.
1단계: 다면체를 펼쳐보기
먼저, 다면체의 한 면을 잘라내고 나머지 면들을 평면 위에 펼쳐 놓는다고 생각해 보세요. 마치 종이접기를 펼치듯이 말이죠. 이때 꼭짓점과 모서리의 개수는 변하지 않지만, 면의 개수는 잘라낸 한 면만큼 줄어들게 되겠죠? 그러면 이 펼쳐진 도형에서 V - E + F = 1이 되는 걸 확인할 수 있어요.
2단계: 삼각형으로 분할하기
다음으로, 펼쳐진 도형을 삼각형으로 쪼개 보는 거예요. 삼각형이 아닌 다각형이 있다면 대각선을 그어서 삼각형으로 만들면 되죠. 이 과정에서 모서리와 면의 개수는 변하지만, V - E + F의 값은 항상 1을 유지한답니다.
3단계: 삼각형 하나씩 없애기
이제 삼각형으로만 이루어진 도형이 되었어요. 이 도형에서 삼각형을 하나씩 없애 보면서 V - E + F의 값이 어떻게 변하는지 살펴보세요. 삼각형을 없앨 때마다 모서리와 꼭짓점의 개수가 변하지만, V - E + F의 값은 변하지 않고 항상 1을 유지한답니다.
4단계: 마지막 삼각형
결국에는 삼각형 하나만 남게 되는데, 이 마지막 삼각형에서도 V - E + F = 1이 성립해요. 그리고 이 1에 처음에 잘라냈던 면을 다시 더해주면, 최종적으로 V - E + F = 2가 되는 거랍니다.
어때요? 이 증명 과정을 통해 오일러 공식이 왜 항상 성립하는지 조금 이해가 되었나요?
오일러의 정리: 위상수학으로의 확장
위상수학과 오일러 수

오일러의 다면체 정리는 단순히 다면체의 성질을 설명하는 것 이상의 의미를 지니고 있어요. 바로 위상수학이라는 새로운 수학 분야의 기초를 마련했기 때문이죠. 위상수학은 도형의 크기나 모양이 아닌, 연결 상태와 같은 본질적인 성질을 연구하는 학문이에요.
오일러의 다면체 정리에서 나타나는 값 V - E + F를 오일러 수라고 부르는데, 이 값은 다면체의 모양이 변형되더라도 항상 일정하게 유지된다는 특징이 있어요. 예를 들어, 정육면체를 아무리 찌그러뜨리거나 늘려도 꼭짓점, 모서리, 면의 개수 사이의 관계는 변하지 않고 오일러 수는 항상 2를 유지한답니다.
도넛과 커피잔: 위상수학의 신비

이러한 위상 불변량의 개념은 위상수학에서 매우 중요해요. 위상수학에서는 도형의 크기나 모양은 중요하지 않고, 연결 상태만 중요하게 생각하거든요. 예를 들어, 도넛과 커피잔은 모양은 다르지만, 구멍이 하나씩 뚫려 있다는 공통점을 가지고 있죠. 이러한 공통점 때문에 위상수학에서는 도넛과 커피잔을 같은 종류의 도형으로 분류한답니다.
오일러의 정리, 고차원으로 확장하다
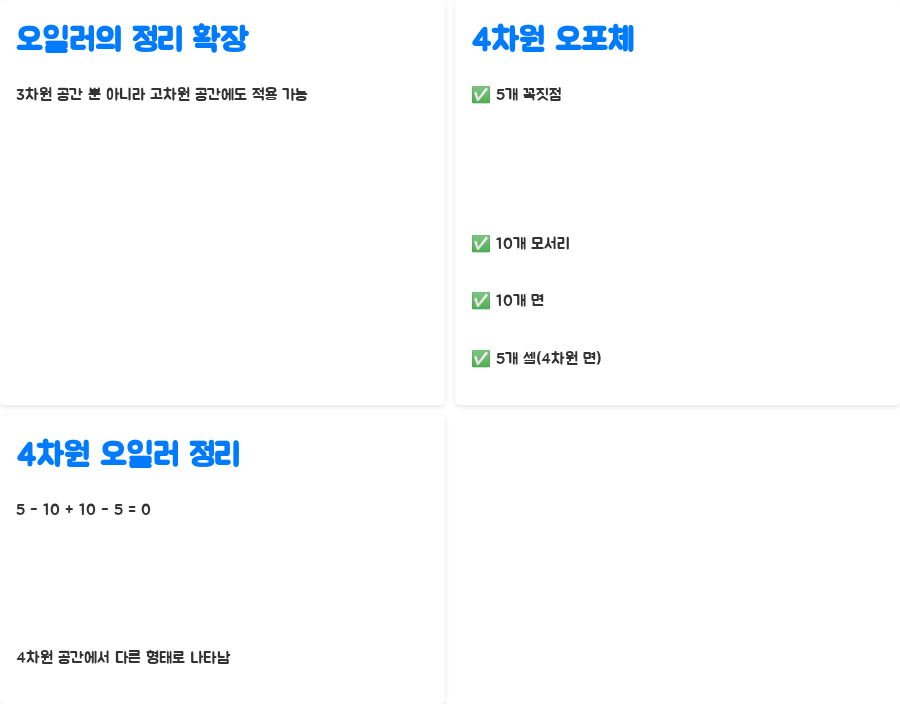
오일러의 정리는 3차원 공간뿐만 아니라 고차원 공간으로 확장하여 적용할 수도 있어요. 4차원 공간의 다면체인 오포체를 생각해 볼까요? 오포체는 5개의 꼭짓점, 10개의 모서리, 10개의 면, 5개의 셀(4차원 공간에서의 면에 해당)로 이루어져 있어요. 이 값들을 오일러의 정리에 대입하면 5 - 10 + 10 - 5 = 0이 되는데, 이는 4차원 공간에서 오일러의 정리가 조금 다른 형태로 나타난다는 것을 의미하죠.
오일러 공식의 활용: 다양한 분야에서 빛나는 공식
정다면체의 비밀: 오일러 공식으로 풀어내다

오일러의 다면체 정리는 정다면체의 개수를 찾는 데에도 사용될 수 있어요. 정다면체는 모든 면이 합동인 정다각형으로 이루어져 있고, 각 꼭짓점에 모이는 면의 개수가 같은 다면체를 말하죠. 오일러 공식과 정다면체의 조건을 이용하면, 정다면체는 오직 5가지(정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체)뿐이라는 것을 증명할 수 있답니다.
다면체의 각: 면각 결손과 오일러 공식
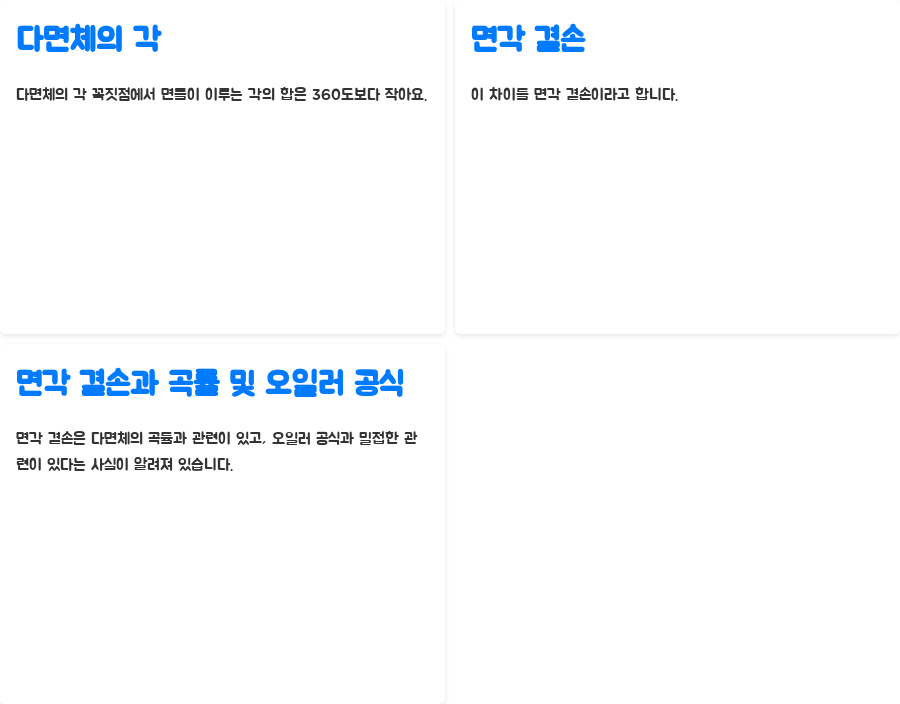
다면체의 각 꼭짓점에서 면들이 이루는 각의 합은 360도보다 작아요. 이 차이를 면각 결손이라고 하는데, 이 면각 결손은 다면체의 곡률과 관련이 있고, 오일러 공식과 밀접한 관련이 있다는 사실이 알려져 있답니다.
오일러 공식을 활용한 문제 풀이

다음은 오일러 공식을 활용하여 다면체의 특징을 알아내는 문제의 예시입니다.
문제:
어떤 다면체의 꼭짓점이 6개이고, 면이 5개일 때, 모서리의 개수는 몇 개일까요?
풀이:
오일러 공식 V - E + F = 2에 V = 6, F = 5를 대입하면, 6 - E + 5 = 2가 됩니다. 따라서 E = 9가 되므로, 모서리의 개수는 9개라는 것을 알 수 있습니다.
| 정사면체 | 4 | 6 | 4 | 2 |
| 정육면체 | 8 | 12 | 6 | 2 |
| 정팔면체 | 6 | 12 | 8 | 2 |
| 정십이면체 | 20 | 30 | 12 | 2 |
| 정이십면체 | 12 | 30 | 20 | 2 |
다면체 꼭짓점(V) 모서리(E) 면(F) 오일러 수(V-E+F)
QnA 섹션

Q1. 오일러의 다면체 정리는 어떤 다면체에 적용될 수 있나요?
A1. 오일러의 다면체 정리는 모든 볼록 다면체에 적용됩니다. 볼록 다면체는 어떤 두 점을 연결하는 선분이 항상 다면체 내부에 포함되는 다면체를 말해요.
Q2. 오일러 수는 무엇이고 왜 중요한가요?
A2. 오일러 수는 오일러의 다면체 정리에서 계산되는 값 (V - E + F)이고, 다면체의 위상적 특징을 나타내는 중요한 값이에요. 오일러 수는 다면체의 모양이 변형되더라도 항상 일정하게 유지되기 때문에 위상 불변량이라고 부르죠.
Q3. 오일러의 다면체 정리는 어떻게 증명되나요?
A3. 오일러의 다면체 정리는 다양한 방법으로 증명될 수 있지만, 대표적인 방법으로는 다면체를 펼치고 삼각형으로 분할하는 방법이 있어요. 이 방법은 다면체의 면을 하나씩 제거하면서 꼭짓점, 모서리, 면의 개수가 어떻게 변하는지 분석하는 방식으로 증명을 진행한답니다.
마무리하며
오일러의 다면체 정리는 다면체의 기본적인 성질을 설명하는 중요한 정리이지만, 그 의미는 여기서 그치지 않아요. 위상수학의 기초를 이루는 핵심 개념이며, 다양한 분야에서 활용될 수 있는 힘을 지니고 있답니다. 오일러 공식을 통해 우리는 다면체의 겉모습뿐만 아니라 그 이면에 숨겨진 수학적 아름다움과 신비를 발견할 수 있죠.
앞으로도 다면체의 세계를 탐험하며 오일러의 정리가 어떻게 활용되는지 탐구해 보는 건 어떨까요?
키워드 다면체,오일러,오일러공식,기하학,위상수학,수학,수학공식,볼록다면체,정다면체,오일러수,위상불변량,수학개념,고차원,오포체,면각결손,데카르트,수학탐구,서울대,심층면접,구술면접,기출문제,수학문제,문제풀이,수학공부,수학강의,수학스타그램,공부스타그램


댓글